The sum of the exponents of the concentration terms in the rate expression is known as the order of reaction.
For homogeneous reaction,
mA + nB = Product
Rate of reaction,
Overall order of entire reaction = (m + n)
Order of reaction with respect to A = m
Order of reaction with respect to B = n
For the rate expression of
Reaction is zero order if n = 0
Reaction is 1st order if n = 1
Reaction is 2nd order if n = 2
Zero order reaction:
A reaction is of zero order when the rate of reaction is independent of the concentration of materials. The rate of reaction is a constant. When the limiting reactant is completely consumed, the reaction stops abruptly.
The zero order rate law for the general reaction
The zero order rate law for the general reaction
At = Final concentration by fading at time t
If, Ao = c and after time t the amount of reactant reacted is x then,
At = c – x
Putting this values in no 1 equation,
C –x = c - kot
X = kot………………………………………………………….2
Half life of zero order reaction:
Half life is defined as the time required for concentration of a reactant to decrease to half of its initial value;
When;
From zero order rate expression,
First order reaction:
In first order reaction, the rate of reaction is proportional to the concentration of one of the reactants.

It is called first order reaction.
Rate expression:
For first order reaction
A→ product.
Where the equilibrium conc. Of A is c,
Then,

The value of k:

Half life of first order reaction:

Second order reaction:
The rate of a second order reaction is proportional to either the concentration of a reactant squared, or the product of concentrations of two reactants.
For the general case of a reaction between A and B, such that

the rate of reaction will be given by
the rate of reaction will be given by

A plot of 1 / [A] vs t produces a straight line with slope k and intercept 1 / [A]0 . The plot should be linear up to a conversion of about 50%.
2. Starting concentrations of the two reactants are different: If [A]0 and [B]0 are different the variable x is used.
Equation (1) becomes
where [A]0 - x = [A], [B]0 - x = [B] and x is the decrease in the concentration of A and B.
Equation (5) can be integrated after separation of the variables and partial fraction expansion. The result is:

where C is the constant of integration.
Using the condition that x = 0, when t = 0, the value of C can be found

If the experimental method yields reactant concentrations rather than x, the equivalent form of equation (8) is;
Because equivalent amounts of A and B are reacting, [A] can be expressed in terms of [B].
If [B] = x , [A] = [A]0 - (x0 - x)
Provided that the initial concentration of A is twice the initial concentration of B
If [B] = x , [A] = [A]0 - (x0 - x)
Provided that the initial concentration of A is twice the initial concentration of B

References:
1. Physical Chemistry
(Peter Atkins, Julio De Paula)
2. Wikipedia
3. A Textbook of Physical Chemistry
(K K Sharma)
4. Physical Chemistry
(Thomas Engel)
1. Physical Chemistry
(Peter Atkins, Julio De Paula)
2. Wikipedia
3. A Textbook of Physical Chemistry
(K K Sharma)
4. Physical Chemistry
(Thomas Engel)







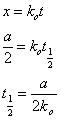





No comments:
Post a Comment